The idea behind the square tracing algorithm is very simple; this could be attributed to the fact that the algorithm was one of the first attempts to extract the contour of a binary pattern.
To understand how it works, you need a bit of imagination...
Given a digital pattern i.e. a group of black pixels, on a background of white pixels i.e. a grid; locate a black pixel and declare it as your "start" pixel. (Locating a "start" pixel can be done in a number of ways; we'll start at the bottom left corner of the grid, scan each column of pixels from the bottom going upwards -starting from the leftmost column and proceeding to the right- until we encounter a black pixel. We'll declare that pixel as our "start" pixel.)

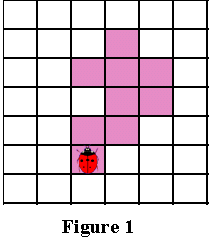
Now, imagine that you are a bug (ladybird) standing on the start pixel as in Figure 1 below. In order to extract the contour of the pattern, you have to do the following:
every time you find yourself standing on a black pixel, turn left, and
every time you find yourself standing on a white pixel, turn right,
until you encounter the start pixel again.
The black pixels you walked over will be the contour of the pattern.

The important thing in the square tracing algorithm is the "sense of direction". The left and right turns you make are with respect to your current positioning, which depends on the way you entered the pixel you are standing on. Therefore, it's important to keep track of your current orientation in order to make the right moves.
 

Algorithm

The following is a formal description of the square tracing algorithm:

Input: A square tessellation, T, containing a connected component P of black cells.

Output: A sequence B (b₁, b₂ ,..., b_k) of boundary pixels i.e. the contour.

Begin

• Set B to be empty.
• From bottom to top and left to right scan the cells of T until a black pixel, s, of P is found.
• Insert s in B.
• Set the current pixel, p, to be the starting pixel, s.
• Turn left i.e. visit the left adjacent pixel of p.
• Update p i.e. set it to be the current pixel.
• While p not equal to s do

   If the current pixel p is black
• insert p in B and turn left (visit the left adjacent pixel of p).
• Update p i.e. set it to be the current pixel.
   else
• turn right (visit the right adjacent pixel of p).
• Update p i.e. set it to be the current pixel.
end While

Note: The notion of left and right in the above algorithm is not to be interpreted with respect to the page or the reader but rather with respect to the direction of entering the "current'' pixel during the execution of the scan.
 
 
 

Demonstration

The following is an animated demonstration of how the square tracing algorithm proceeds to trace the contour of a given pattern. Remember that you are a bug (ladybird) walking over the pixels; notice how your orientation changes as you turn left or right. Left and right turns are made with respect to your current positioning on the pixel i.e. your current orientation.

Analysis

It turns out that the square tracing algorithm is very limited in its performance. In other words, it fails to extract the contour of a large family of patterns which frequently occur in real life applications.
This is largely attributed to the left and right turns which tend to miss pixels lying "diagonally" with respect to a given pixel.
We will examine different patterns of different connectivity and see why the square tracing algorithm fails. In addition, we will examine ways in which we can improve the performance of the algorithm and make it at least work for patterns with a special kind of connectivity.
 

The Stopping Criterion

One weakness of the square tracing algorithm lies in the choice of the stopping criterion. in other words, when does the algorithm terminate?
In the original description of the square tracing algorithm, the stopping criterion is visiting the start pixel for a second time. It turns out that the algorithm will fail to contour trace a large family of patterns if it were to depend on that criterion.
What follows is an animated demonstration explaining how the square tracing algorithm fails to extract the contour of a pattern due to the bad choice of the stopping criterion:
 
 

As you can see, improving the stopping criterion would be a good start to improving the overall performance of the square tracing algorithm. There are 2 effective alternatives to the existing stopping criterion:

a) Stop after visiting the start pixel n times, where n is at least 2, OR
b) Stop after entering the start pixel a second time in the same manner you entered it initially. This criterion was proposed by Jacob Eliosoff and we will therefore call it Jacob's stopping criterion.

Changing the stopping criterion will generally improve the performance of the square tracing algorithm but will not allow it to overcome other weaknesses it has towards patterns of special kinds of connectivity.
 
 

The Square Tracing Algorithm fails to trace the contour of a family of  8-connected patterns that are NOT 4-connected

The following is an animated demonstration of how the square tracing algorithm (with Jacob's stopping criterion)  fails to extract the contour of an 8-connected pattern that's not 4-connected:
 
 

Is the Square Tracing Algorithm completely useless?

If you have read the analysis above you must be thinking that the square tracing algorithm fails to extract the contour of most patterns. It turns out that there exists a special family of patterns which are completely and correctly contour traced by the square tracing algorithm.
Let P be a set of 4-connected black pixels on a grid. Let the white pixels of the grid i.e. the background pixels, W, also be 4-connected. It turns out that given such conditions of the pattern and its background, we can prove that the square tracing algorithm (using Jacob's stopping criterion) will always succeed in extracting the contour of the pattern.

The following is a proof when both pattern and background pixels are 4-connected, the square tracing algorithm will correctly extract the contour of the pattern provided we use Jacob's stopping criterion.
 

Proof

Given: A  pattern, P, such that both the pattern pixels i.e. the black pixels, and the background pixels i.e. the white pixels, W, are 4-connected.

First Observation
Since the set of white pixels, W, are assumed to be 4-connected, this means that the pattern cannot have any "holes" in it.
(informally, "holes" are groups of white pixels which are completely surrounded by black pixels in the given pattern).
The presence of any "hole" in the pattern will result in disconnecting a group of white pixels from the rest of the white pixels and therefore making the set of white pixels not 4-connected.
Figure 2 and Figure 3 below demonstrate 2 kinds of "holes" that could occur in a 4-connected pattern:

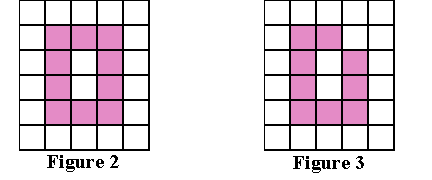
Second Observation
Any two black pixels of the pattern MUST share a side.
Say that 2 black pixels only share a vertex, then, in order to satisfy the 4-connectedness property of the pattern, there should be a path linking those 2 pixels such that every 2 adjacent pixels in that path are 4-connected. But this will give us a pattern similar to the one in Figure 3 above. In other words, this would cause the white pixels to become disconnected.
Figure 4 below demonstrates a typical pattern satisfying the assumption that both background and pattern pixels are 4-connected i.e. no "holes" and every 2 black pixels share a side:

A useful way of picturing such patterns is:
First, consider the boundary pixels i.e. the contour, of the pattern. Then, if we consider each boundary pixel as having 4 edges each of unit length, we'll see that some of these edges are shared with adjacent white pixels. We'll call these edges i.e. the ones shared with white pixels, boundary edges.
These boundary edges could be viewed as edges of a polygon. Figure 5 below demonstrates this idea by showing you the polygon corresponding to the pattern in Figure 4 above:

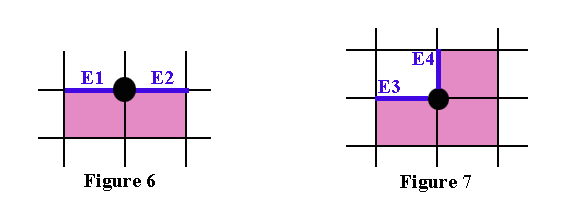
If we look at all possible "configurations" of boundary pixels that could arise in such patterns, we'll see that there are 2 basic cases displayed in Figure 6 and Figure 7 below.
Boundary pixels may be multiples of these cases or different positionings i.e. rotations of these 2 cases.
The boundary edges are marked in blue as E1, E2, E3 and E4.

Third Observation
For both the above 2 cases, no matter which pixel you choose as your start pixel and no matter what direction you enter it, the square tracing algorithm will never "backtrack", will never "go through" a boundary edge twice (unless it's tracing the boundary for a second time) and will never miss a boundary edge...try it!
2 concepts need to be clarified here:
a) the algorithm "backtracks" when it goes backwards to visit an already visited pixel before tracing the whole boundary, and
b) for every boundary edge there are 2 ways to "go through" it, namely "in" or "out" (where "in" means towards the inside of the corresponding polygon and "out" means towards the outside of the polygon).

In addition, when the square algorithm goes "in" through one of the boundary edges, it will go "out" through the next boundary edge i.e. it can't be possible for the square tracing algorithm to go through 2 consecutive boundary edges in the same manner.
 

Final Observation
There is an even number of boundary edges for any given pattern.
If you take a look at the polygon of Figure 5 above, you'll see that:
if you want to start at vertex S, marked on the diagram, and follow the boundary edges until you reach S again; you'll see that you'll pass by an even number of boundary edges in the process. Consider each boundary edge as a "step" in a given direction. Then, for every "step" to the right, there should be a corresponding "step" to the left if you want to go back to your original position. The same applies to vertical "steps" . As a result, the "steps" should be matching pairs and this explains why there would be an even number of boundary edges in any such pattern.

As a result, when the square tracing algorithm enters the start boundary edge (of the start pixel) for a second time, it will do so in the same direction it did when it first entered it.
The reason for that is since there are 2 ways to go through a boundary edge, and since the algorithm alternates between "in" and "out" of consecutive  boundary edges, and since there is an even number of boundary edges, the algorithm will go through the start boundary edge a second in the same manner it did the first time around.
 

Conclusion
Given a 4-connected pattern and background, the square tracing algorithm will trace the whole boundary i.e. contour, of the pattern and will stop after tracing the boundary once i.e. it will not trace it again since when it reaches the start boundary edge for a second time, it will enter it in the same way it did the first time around.
Therefore, the square tracing algorithm, using Jacob's stopping criterion, will correctly extract the contour of any pattern provided both the pattern and its background are 4-connected.