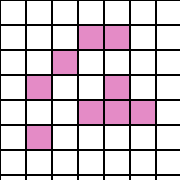Introduction
In binary valued digital imaging, a pixel can either have a value of
1 -when it's part of the pattern- , or 0 -when it's part of the background-
i.e. there is no grayscale level. (We will assume that pixels with value
1 are black while zero valued pixels are white).
In order to identify objects in a digital pattern, we
need to locate groups of black pixels that are "connected" to each other.
In other words, the objects in a given digital pattern are
the connected components of that pattern.
In general, a connected component is a set of black pixels,
P, such that for every pair of pixels pi and pj
in P, there exists a sequence of pixels pi,
..., pj such that:
a) all pixels in the sequence are in the set P i.e. are black,
and
b) every 2 pixels that are adjacent in the sequence are
"neighbors"
As a result, an important question arises: When can we say that
2 pixels are "neighbors"?
Since we are using square pixels, the answer to the previous question
is not trivial. The reason for that is: in a
square tessellation,
pixels either share an edge, a vertex, or neither. There are 8 pixels sharing
an edge or a vertex with any given pixel; these pixels make up the Moore
neighborhood of that pixel. Should we consider pixels having only a
common vertex as "neighbors" ? Or should 2 pixels have a common edge in
order for them to be considered "neighbors"?
This gives rise to 2 types of connectedness, namely: 4-connectivity
and 8-connectivity.
4-Connectivity
When can we say that a given set of black pixels is 4-connected
?
First, we have to define the concept of a 4-neighbor (also
known as a direct-neighbor):
Definition of a 4-neighbor:
A pixel, Q, is a 4-neighbor of a given pixel,
P, if Q and P share an edge.
The 4-neighbors of pixel P (namely pixels P2,P4,P6 and
P8) are shown in Figure 2 below.
Definition of a 4-connected component :
A set of black pixels, P, is a 4-connected component if
for every pair of pixels pi and pj
in P, there exists a sequence of pixels pi,
..., pj such that:
a) all pixels in the sequence are in the set P i.e. are black,
and
b) every 2 pixels that are adjacent in the sequence are
4-neighbors
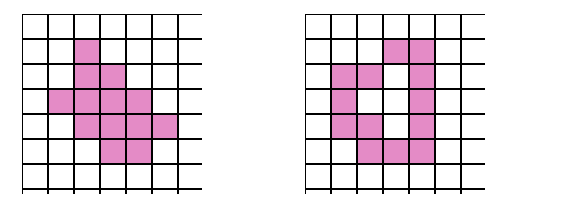
Examples of 4-connected patterns :
The following diagrams are examples of patterns that are 4-connected:
8-Connectivity
When can we say that a given set of black pixels is 8-connected
?
First, we have to define the concept of an 8-neighbor (also
known as an indirect-neighbor):
Definition of an 8-neighbor:
A pixel, Q, is an 8-neighbor (or simply a neighbor)
of a given pixel, P, if Q and P either share an edge
or a vertex.
The 8-neighbors of a given pixel P make up the Moore
neighborhood of that pixel.
Definition of an 8-connected component:
A set of black pixels, P, is an 8-connected component
(or simply a connected component) if for every pair of pixels
pi and pj in P, there exists
a sequence of pixels pi, ..., pj such
that:
a) all pixels in the sequence are in the set P i.e. are black,
and
b) every 2 pixels that are adjacent in the sequence are
8-neighbors
NOTE
All 4-connected patterns are 8-connected i.e. 4-connected patterns
are a subset of the set of 8-connected patterns.
On the other hand, an 8-connected pattern may not be 4-connected.
Example of 8-connected pattern :
The diagram below is an example of a pattern that is 8-connected but
not 4-connected:
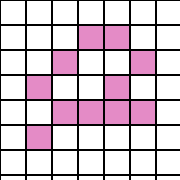
Example of a pattern that's not 8-connected:
The diagram below is an example of a pattern that is not 8-connected
i.e. is made up of more than one connected component (there are 3 connected
components in the diagram below):